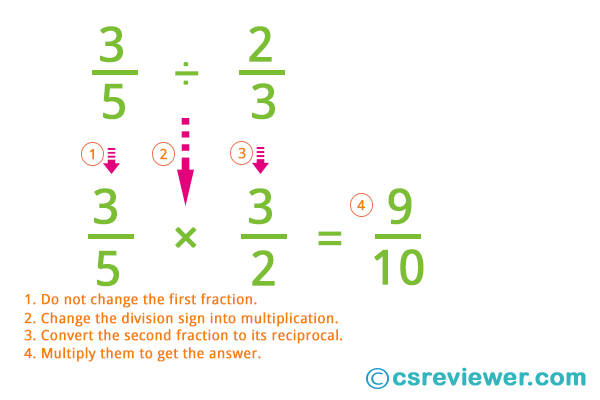
Hi there again and welcome back to CSEReviewer.com. Our next CSC reviewer exercise will be about dividing fractions. Yes, we’re onto division now but if you want to review our previous exercise, then we recommend you take a look at the Multiplying Fractions tutorial and practice questions we posted. Before we proceed and fully understand how dividing fractions work, we first need to learn about RECIPROCALS. A reciprocal is a term used for when you invert a fraction. For example, if you have the fraction 3⁄4 and asked to give its reciprocal, you just go and switch the bottom and top numbers. You will obviously get the fraction 4⁄3.
Time for some sample exercises regarding dividing fractions. There are 20 items in this CSC reviewer that will help you in passing the CSC exam so try to get as many correct answers as possible. If the answer is an improper action, convert it to mixed numbers.
Once you are done answering them, hit any of the social media buttons below for the answers to be revealed, and to check out how you fared in the exercise above.
Here are all the correct answers to our Dividing Fractions exercise questions.
1. 5 3⁄5 = 4/5 ÷ 1/7 can be rewritten as:
4/5 x 7/1.
Then, you can simplify by multiplying the numerators together and the denominators together:
4/5 x 7/1 = (4 x 7)/(5 x 1) = 28/5 => 5 3⁄5.
2. 8 6⁄13 = 11/13 ÷ 1/10 can be rewritten as 11/13 x 10/1.
Then, we can simplify by multiplying the numerators together and the denominators together:
11/13 x 10/1 = (11 x 10)/(13 x 1) = 110/13 or 8 6⁄13 when expressed as a mixed number.
3. 11⁄18 = 4/8 ÷ 9/11 can be rewritten as 4/8 x 11/9.
Then, we simplify by canceling out any common factors between the numerators and denominators:
4/8 can be simplified to 1/2 by dividing both the numerator and denominator by 4.
11 and 9 have no common factors, so they cannot be simplified.
1/2 x 11/9 = (1 x 11)/(2 x 9) = 11⁄18.
4. 36⁄49 = can be written as 6/7 ÷ 14/12 = 6/7 × 12/14
Multiplying the numerators together gives us:
6 × 12 = 72
Multiplying the denominators together gives us:
7 × 14 = 98
Therefore, the result is:
6/7 ÷ 14/12 = 72/98
We can simplify this fraction by dividing both the numerator and denominator by their greatest common factor, which is 2:
72/98 = (72 ÷ 2)/(98 ÷ 2) = 36/49
So the final result is 36⁄49.
5. 1 29⁄35 = We multiply the first fraction by the reciprocal of the second fraction. In this case, we have:
8/5 ÷ 7/8 = 8/5 × 8/7
Next, we multiply the numerators together and the denominators together:
= (8 × 8)/(5 × 7)
Simplifying the numerator and denominator gives:
= 64/35
Therefore, 8/5 ÷ 7/8 is equal to the mixed number 1 29/35 or the improper fraction 64/35.
By converting improper fraction to mixed number, the correct answer is 1 29⁄35.
6. 1 1⁄4 = To divide fractions, we can multiply the first fraction by the reciprocal of the second fraction:
3/6 ÷ 4/10 = 3/6 × 10/4
Now, we can directly multiply the numerators and denominators of the two fractions:
3/6 × 10/4 = (3 × 10) / (6 × 4)
Multiplying the numerator and denominator, we get:
(3 × 10) / (6 × 4) = 30 / 24
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 30 and 24 are divisible by 6, so we can divide both by 6:
30/24 = (30 ÷ 6)/(24 ÷ 6) = 5/4
Therefore, 3/6 ÷ 4/10 simplifies to 5/4 or 1 1⁄4.
7. 2 2⁄7 = We will again multiply the first fraction by the reciprocal of the second fraction:
8/7 ÷ 1/2 = 8/7 × 2/1
Now, we can directly multiply the numerators and denominators of the two fractions:
8/7 × 2/1 = (8 × 2) / (7 × 1)
Multiplying the numerator and denominator, we get:
(8 × 2) / (7 × 1) = 16 / 7
We can convert this improper fraction to a mixed number by dividing the numerator by the denominator:
16/7 = 2 2/7
Therefore, 8/7 ÷ 1/2 is equal to 2 2⁄7.
8. 1 1⁄4 = Multiply the first fraction by the reciprocal of the second fraction:
5/6 ÷ 2/3 = 5/6 × 3/2
Now, we can directly multiply the numerators and denominators of the two fractions:
5/6 × 3/2 = (5 × 3) / (6 × 2)
Multiplying the numerator and denominator, we get:
(5 × 3) / (6 × 2) = 15 / 12
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 15 and 12 are divisible by 3, so we can divide both by 3:
15/12 = (15 ÷ 3)/(12 ÷ 3) = 5/4
Therefore, 5/6 ÷ 2/3 simplifies to 5/4 or 1 1⁄4 as a mixed number.
9. 2 1⁄3 = We will multiply the first fraction by the reciprocal of the second fraction:
7/9 ÷ 1/3 = 7/9 × 3/1
Now, we can directly multiply the numerators and denominators of the two fractions:
7/9 × 3/1 = (7 × 3) / (9 × 1)
Multiplying the numerator and denominator, we get:
(7 × 3) / (9 × 1) = 21 / 9
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 21 and 9 are divisible by 3, so we can divide both by 3:
21/9 = (21 ÷ 3)/(9 ÷ 3) = 7/3
Therefore, 7/9 ÷ 1/3 simplifies to 7/3 or 2 1⁄3 as a mixed number.
10. 1 1⁄5 = Multiply the first fraction by the reciprocal of the second fraction:
2/5 ÷ 4/12 = 2/5 × 12/4
Now, we can directly multiply the numerators and denominators of the two fractions:
2/5 × 12/4 = (2 × 12) / (5 × 4)
Multiplying the numerator and denominator, we get:
(2 × 12) / (5 × 4) = 24 / 20
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 24 and 20 are divisible by 4, so we can divide both by 4:
24/20 = (24 ÷ 4)/(20 ÷ 4) = 6/5
Therefore, 2/5 ÷ 4/12 simplifies to 6/5 or 1 1⁄5 as a mixed number.
11. 2 = Again, multiply the first fraction by the reciprocal of the second fraction:
3/5 ÷ 3/10 = 3/5 × 10/3
Now, we can directly multiply the numerators and denominators of the two fractions:
3/5 × 10/3 = (3 × 10) / (5 × 3)
Multiplying the numerator and denominator, we get:
(3 × 10) / (5 × 3) = 30 / 15
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 30 and 15 are divisible by 15, so we can divide both by 15:
30/15 = (30 ÷ 15)/(15 ÷ 15) = 2/1
Therefore, 3/5 ÷ 3/10 simplifies to 2.
12. 1 1⁄9 = Just like the previous methods, multiply the first fraction by the reciprocal of the second fraction:
10/12 ÷ 3/4 = 10/12 × 4/3
Now, we can directly multiply the numerators and denominators of the two fractions:
10/12 × 4/3 = (10 × 4) / (12 × 3)
Multiplying the numerator and denominator, we get:
(10 × 4) / (12 × 3) = 40 / 36
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 40 and 36 are divisible by 4, so we can divide both by 4:
40/36 = (40 ÷ 4)/(36 ÷ 4) = 10/9
Therefore, 10/12 ÷ 3/4 simplifies to 10/9. However, this is an improper fraction, so we can convert it to a mixed number by dividing the numerator by the denominator and writing the remainder as a fraction:
10/9 = 1 1⁄9.
13. 8 = Multiply the first fraction by the reciprocal of the second fraction:
4/6 ÷ 1/12 = 4/6 × 12/1
Now, we can directly multiply the numerators and denominators of the two fractions:
4/6 × 12/1 = (4 × 12) / (6 × 1)
Multiplying the numerator and denominator, we get:
(4 × 12) / (6 × 1) = 48 / 6
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 48 and 6 are divisible by 6, so we can divide both by 6:
48/6 = (48 ÷ 6)/(6 ÷ 6) = 8/1
Therefore, 4/6 ÷ 1/12 simplifies to 8.
14. 9 1⁄6 = Always multiply the first fraction by the reciprocal of the second fraction:
11/3 ÷ 2/5 = 11/3 × 5/2
Now, we can directly multiply the numerators and denominators of the two fractions:
11/3 × 5/2 = (11 × 5) / (3 × 2)
Multiplying the numerator and denominator, we get:
(11 × 5) / (3 × 2) = 55 / 6
This is an improper fraction, so we can convert it to a mixed number by dividing the numerator by the denominator and writing the remainder as a fraction:
55/6 = 9 1/6
Therefore, 11/3 ÷ 2/5 simplifies to 9 1⁄6.
15. 1 1⁄3 = Multiply the first fraction by the reciprocal of the second fraction:
4/6 ÷ 1/2 = 4/6 × 2/1
Now, we can directly multiply the numerators and denominators of the two fractions:
4/6 × 2/1 = (4 × 2) / (6 × 1)
Multiplying the numerator and denominator, we get:
(4 × 2) / (6 × 1) = 8 / 6
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 8 and 6 are divisible by 2, so we can divide both by 2:
8/6 = (8 ÷ 2)/(6 ÷ 2) = 4/3
Therefore, 4/6 ÷ 1/2 simplifies to 4/3 and 4/3 as a mixed number is 1 1⁄3.
16. 9 = Multiply the first fraction by the reciprocal of the second fraction:
3/4 ÷ 1/12 = 3/4 × 12/1
Now, we can directly multiply the numerators and denominators of the two fractions:
3/4 × 12/1 = (3 × 12) / (4 × 1)
Multiplying the numerator and denominator, we get:
(3 × 12) / (4 × 1) = 36 / 4
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 36 and 4 are divisible by 4, so we can divide both by 4:
36/4 = (36 ÷ 4)/(4 ÷ 4) = 9/1
Therefore, 3/4 ÷ 1/12 simplifies to 9.
17. 8 = As always with dividing fractions, we first multiply the first fraction by the reciprocal of the second fraction:
9/3 ÷ 3/8 = 9/3 × 8/3
Now, we can directly multiply the numerators and denominators of the two fractions:
9/3 × 8/3 = (9 × 8) / (3 × 3)
Multiplying the numerator and denominator, we get:
(9 × 8) / (3 × 3) = 72 / 9
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 72 and 9 are divisible by 9, so we can divide both by 9:
72/9 = (72 ÷ 9)/(9 ÷ 9) = 8/1
Therefore, 9/3 ÷ 3/8 simplifies to 8.
18. 1 22⁄27 = Multiply the first fraction by the reciprocal of the second fraction:
7/9 ÷ 3/7 = 7/9 × 7/3
Now, we can directly multiply the numerators and denominators of the two fractions:
7/9 × 7/3 = (7 × 7) / (9 × 3)
Multiplying the numerator and denominator, we get:
(7 × 7) / (9 × 3) = 49 / 27
Since the resulting fraction is already in its simplest form, we don’t need to simplify it any further.
Therefore, 7/9 ÷ 3/7 simplifies to 49/27 and 49/27 to mixed number is 1 22⁄27.
19. 3 = Multiply the first fraction by the reciprocal of the second fraction:
12/5 ÷ 4/5 = 12/5 × 5/4
Now, we can directly multiply the numerators and denominators of the two fractions:
12/5 × 5/4 = (12 × 5) / (5 × 4)
Multiplying the numerator and denominator, we get:
(12 × 5) / (5 × 4) = 60 / 20
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 60 and 20 are divisible by 20, so we can divide both by 20:
60/20 = (60 ÷ 20)/(20 ÷ 20) = 3/1
Therefore, 12/5 ÷ 4/5 simplifies to 3.
20. 1 5⁄7 = Multiply the first fraction by the reciprocal of the second fraction:
9/7 ÷ 3/4 = 9/7 × 4/3
Now, we can directly multiply the numerators and denominators of the two fractions:
9/7 × 4/3 = (9 × 4) / (7 × 3)
Multiplying the numerator and denominator, we get:
(9 × 4) / (7 × 3) = 36 / 21
We can simplify this fraction by finding a common factor for the numerator and denominator. Both 36 and 21 are divisible by 3, so we can divide both by 3:
36/21 = (36 ÷ 3)/(21 ÷ 3) = 12/7
Therefore, 9/7 ÷ 3/4 simplifies to 12/7 and 12/7 as a mixed number is 1 5⁄7.
I hope you got 17 or more correct answers. If you had trouble with the Dividing Fractions test questions, you should check out this converting improper fractions to mixed numbers tutorials. It will make you understand better the final answers from these exercises.
 Free CSE Reviewers Free Civil Service Exam Reviewer Online and Downloads
Free CSE Reviewers Free Civil Service Exam Reviewer Online and Downloads


